Q: How do we solve composition of transformation problems?:


A: To do a composition of transformations problem correctly 
First ,you must do the second transformation first and then the first  transformation second. (shown in figure1)

Figure 1

In this case you would do the translation(3 ,4) first then the reflection R x-axis second

        NOW YOU TRY :

Given triangle ABC:

A(1,4), B(3,7), C(5,1)

Graph and label the following composition:

Q: How do we use the other definitons of transformations?

A there are different types of transformation like dilation,rotation, reflection and translation.

Though all these types of transformation fall under certain categories like 

Isometry

Glide reflection

         And 

                Orientation

ISOMETRY: 
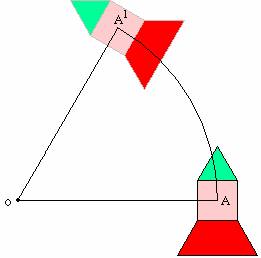
An isometric transformation which is also referred to isometry transformation. In this transformation the figure which is in this case a triangle, can be moved anywhere around the plane and can keep the figure to have  the same lenght no matter where it is on the plane.

GLIDE REFLECTION

Is the combination of both a reflection and a translation that move along a line. 

Figure 1:
Shows how the man in the left is the original copy where it  is translated and then reflected along a line.

Orientation:

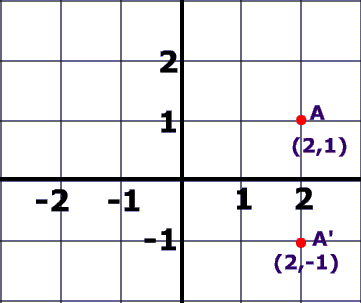
Is the arrangement of the plotted points after a transformation. 

Counterclockwise is a word used to describe orientation because it describes when the points are in opposite ways from the original form. This orientation where the order changes is called opposite isometry.

 Clockwise is when both figures have the same clockwise view after the figure has gone through a transformation. 
This clockwise orientation is also called direct isometry where the same length and same orientation is preserved. 

TRY IT :D 

 

 Does the figure above have an opposite or same orientation ?

                           

1. same 

2 . opposite orientation

Q: How do we identify compositions of transformations?


A:
      Composition of transformations are when two transformations are put together to get a transformation.
 The compositions of transformations are problems that have two or maybe more transformation put together.
An example problem of a composition problem is shown below :

NOW TRY IT :D

WHICH IS A COMPOSITION OF TRANSFORMATIONS?

1. Rx-axis
2. D7
3. R90
4. D7 o R180

Q: How do we identify transformations 


A:  To first understand this question we have to ask ourselves

WHAT ARE TRANSFORMATIONS ?

Transformations is when we move a geometric figure .

we have different kinds of transformations like 

• Translation  

• Dilation

• Rotation

• Reflection

These types of transformation all have different thing that move the figure in a different way.


Translation: 
A translation is when every point is move to a same distance as well as the same directions.


For example: figure one would be a translation because each coordinates are moved at the same time and direction. 

 this would usually be in unites saying it will go either left, right or down and up.

Dilation's is when a shape or image is enlarged or reduction on the size of the image. 

Rotation : Is when a figure is turned around a single point. 

Reflection  : Is a figure is flipped over a line  of symmetry . 

Try this out ;D

Which of the flowing transformations are shown?

1)  Dilation 
2) Reflection
3) Rotation
4) Translation

Q: How do we graph transformations that are reflections?


A: When graphing a transformations like a reflection there has to always be a line a symmetry.
a line of symmetry is a line that can make an exact replica of a figure like the butterfly below in figure one.

       Figure 1.
A reflection  is a figure that has a mirrior image.


when reflecting over x-axis or y-axis there is a rule to how to reflect them.
Reflecting over the X-axis means that the y coordinate has to be flipped.
For example: (x,y) reflected over the x-axis would be (x,-y)


To reflect over the y-axis the x coordinate would have to be flipped.
for example : (x,y) means (-x,y)


Example :
(-1,2) reflected over the x-axis would be (-1,-2) due to the fact that when reflecting over the x-axis the y coordinates changes the sign .

NOW YOU TRY IT :D

Reflect point (2,2) into the x-axis

    A.(-2,2)                   C. (2,2)                       

    B. (2,-2)                  D. (-2,-2)