Melissa's geometry blog

March 15,2012

AIM: How do we find the area of parallelograms, kite and trapezoids ?

PARALLELOGRAM:
To find the area of a parallelogram
is like finding the are of a rectangle .

For the parallelogram we need to first cut a line in the parallelogram where it forms a triangle. in the image to the left parallelogram ABED we cut a line from A to C with that forming triangle we place the triangle to the other side forming a rectangle ACFD.

FORMULA: B x H

-----------------------------------------------------------

EXAMPLE:

Find the are of a parallelogram with a base of 12 centimeters and a height of 5 centimeters.
First : Apply the formula A=BH Then : plug in the base and height: A=125 solve the equation: A= 60cm2 ------------------------------------------------------------------------------ TRAPEZOID : Formula : A= (B1+B2)H 2 B stands for base H for height A for area ----------------------------------------------------------------------------- Example: First: write the formula : A= ( B1+B2)H 2 Plug in numbers: A= (10+14)5 2 Solve : A=( 24)5 2 A= 120 2 A= 60 in2 ------------------------------------------------------------------------------ Kite: 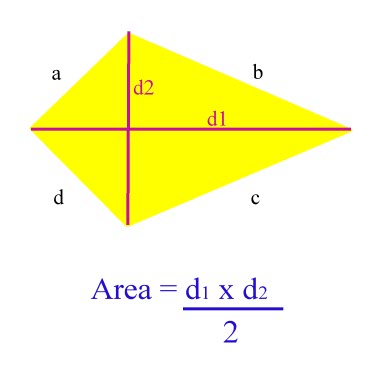WHAT THE PICTURE SHOWS: it shows the formula for the are of a kite D1 and D2 of the kite are shown. ------------------------------------------------------------------------------- EXAMPLE: First: rewrite the formula : A= D1D2 2 SECOND: PLUG IT IN A= D1+D2 2 A= 102 2 Solve the equation : A= 20 = 10 2 Answer A=10 ------------------------------------------------------------------------------ TRY IT: 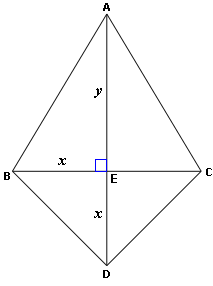Find the area of the kite. Measurements shown are in cm. [Given x = 12 and y = 16.] Sources used : Try it : http://www.icoachmath.com/math_dictionary/Kite.html kite: http://www.k6-geometric-shapes.com/image-files/formula-area-kite.jpg Trapezoid: